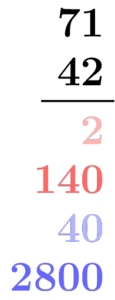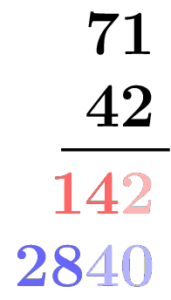Truth and consequences: talking about solving equations

/ Bill McCallum / 1 Comment

The language we use when we talk about solving equations can be a bit of a minefield. It seems obvious to talk about an equation such as $3x + 2 = x + 5$ as saying that $3x+2$ is equal to $x + 5$, and that’s probably a good place to start. But there is a hidden assumption in there that the equation is true. In the Illustrative Mathematics middle school curriculum coming out this month we start students out with hanger diagrams to represent such equations:

The fact that the hanger is balanced embodies the hidden assumption that the equation is true. It is helpful for explaining why you have to perform the same operation on each side when solving equations; if you take two triangles from the left side you have to take two triangles from the right side as well in order to preserve the balance. This leads to a discussion of how performing the same operation on each side of an equation preserves the truth of the equal sign.

But what happens with an equation like $3x + 2 = 3x + 5$? In this case, the hanger diagram is a physical impossibility: the right hand side will always be heavier than the left hand side. I can imagine that students who have an idea of an equation as “the left hand side is equal to the right hand side” might be confused by this situation, and think this is not a proper equation. Especially when they reduce it to $2 = 5$. Students learn to say that this means there are no solutions, but it’s hard to make sense of that response rule without understanding what’s really going on with equations.

The fact is, an equation with a variable in it is neither true nor false, because it is merely a phrase in a longer sentence, such as “If $3x + 2 = x + 5$ then $x = \frac32$.” This sentence is true, but the phrases within it are not sentences and have no inherent truth or falsity. When we perform the same operation on each side of an equation, we are not only preserving the truth of the equal sign but also preserving the consequences of the equal sign. If we use if-then language when talking about equations, then we can make sense of equations with no solutions. A sentence like “If $x$ is a number satisfying $3x + 2 = 3x + 5$ then $2 = 5$” makes perfect sense. It’s the mathematical equivalent of “If the moon is green cheese, then I’m a monkey’s uncle.” It’s a way of saying the moon is not green cheese . . . or that there is no solution to the equation.

The middle schooler’s version of if-then language might not always use the words “if” and “then.” You might say “Imagine there is a number $x$ such that $3x + 2 = x + 5$. What can you say about $x$?” Just as you say “Imagine this hanger is balanced and the green triangles weigh one gram. How much do the blue squares weigh?” I think it’s a useful approach with students to remember that equations are a matter not just of truth, but of truth and consequences.

Why is a negative times a negative a positive?

/ Bill McCallum / 15 Comments

OK, I can hear the groans already. There are many contexts for answering this question and they are dubious in varying degrees because the real answer is “because I said so.” That is to say, the rule for multiplying negatives is a convention; adopted for good reasons, but a convention nonetheless. Those good reasons are mathematical: we want to make sure that when we extend multiplication and addition to negative numbers the properties of operations still apply. In particular, we want the distributive property to apply. Meditate on this:
$$
3\cdot(5 + (-5)) = 3\cdot5 + 3 \cdot (-5).
$$
The left side is really $3 \cdot 0$, so it had better be zero. So the right side had better be zero as well. The first term on the right side is 15, so the other term had better be $-15$. So $3 \cdot (-5) = -15$. We want the commutative law to hold, so we had better say $(-5)\cdot 3 = -15$ as well. Now meditate on
$$
(-5)\cdot(3 + (-3)) = (-5)\cdot 3 + (-5)\cdot(-3).
$$
The same reasoning tells us that $(-5)\cdot(-3) = 15$.

Trouble is, all this is really hard to explain to middle schoolers, so people invent contexts. One context I’ve seen has something to do with sending out bills. If you receive 5 bills for 3 dollars then you have $5 \cdot (-3) = -15$ dollars. Sending out is the opposite of receiving, so if you send out 5 bills for 3 dollars, you have $(-5)(-3)$ dollars. But once you receive payment, you have \$15. So $(-5)(-3) = 15$.

One problem with this is that you have to buy more conventions to believe it: the convention about negative amounts of money representing debt, the convention about negative receiving being kinda sorta like sending out. That’s a lot of conventions to prove something that is, as I said, a convention itself. Another problem is that all this context really shows is that $-(-3) = 3$, five times. The multiplication in this context is really just repeated addition; it doesn’t work for numbers that are not integers. You can’t send out 5.6 bills.

There is one context that I think does a better job here, and that is $\mbox{distance} = \mbox{speed} \times \mbox{time}$. This does work with non-integers, and you can make sense of all of the quantities involved as negative numbers. Let’s assume that an object is moving along the number line, and that you measure its position at different times, setting your stop watch to 0 when it passes through the origin. Negative distance is distance to the left; negative speed is speed from right to left; and negative time is time before you started measuring. (Later we use the terms displacement and velocity, but there’s no need to introduce them right away.)

So if the object is moving at $-5$ m/sec, where is it at time $-3$ seconds? Well, it’s moving from right to left and it has 3 seconds before it hits the origin, so it is 15 m to the right of the origin. So $(-5)(-3) = 15$.

Was I cheating there? Is this context subject to the same objections I made about the money context? Didn’t I just make up a whole bunch of conventions about negative distance, time, and speed? I think these conventions pass the cognitive sniff test better. They don’t seem as artificial to me. You can really make quantitative sense of negative distance, speed, and time. It feels more like the real world and less like an accountant’s convention. (No offense to accountants intended.) In a way, we have replaced the mathematician’s desire to have the properties of operations continue to hold with the physicist’s desire to have the laws of physics continue to hold.

So where is the distributive property in all of this? I think it is built into our physical intuition about this context. If I travel for 3 hours, and then for another 2 hours, I can figure out how far I have gone by just adding the times and multiplying by my speed, or I can add the distances traveled in each time period. That’s the distributive property. If you dig into the reasoning I gave for the object moving at $-5$ m/sec in the light of this common sense, questioning each claim, you end up with something not too far from the mathematical reasoning I gave earlier.

By the way, this is the approach we take in the Illustrative Mathematics middle school curriculum. Finding contexts for mathematical ideas that are faithful to the mathematics is difficult and requires real sensitivity to both the mathematics and the way students think. Our brilliant curriculum writing team is up to that challenge.

Talking about fractions, decimals, and numbers

/ Bill McCallum / 3 Comments

When students first learn about fractions, we want them to learn that they are just numbers; new numbers, but numbers nonetheless, that fit into the same system as the whole numbers they are familiar with. The number line can help with this, with whole numbers and fractions sitting together, and located in essentially the same way; choose a unit (1, 1/3, 1/10) and then count off a number of those units. It also helps students understand that equivalent fractions are just different ways of writing the same number. When (finite) decimals come along, they get added to the list of representations.

The Common Core emphasizes this unity by treating decimals as just a different way of writing fractions, e.g. in 4.NF.C: “Understand decimal notation for fractions, and compare decimal fractions.” In this view, 0.3 is not a new sort of number, just a different way of writing the number 3/10.

This leads to some difficulties in the use of language, because at some points in the curriculum you do want to distinguish between decimals and fractions, for example when you ask a student to write 4/5 as a decimal or to write 0.125 as a fraction. (“You told me it’s already a fraction!” the smart student might reply.)

The IM curriculum writing team was talking about these difficulties the other day and Cathy Kessel had a useful comment:

There’s a developmental issue. When fractions are introduced, the distinction between number represented and representation is blurred, and similarly for decimals (finite, then repeating). But, when the two types of representations are seen as representing the same thing, then the thing and its representations start to separate more.

Because we want students to develop a conception of the number behind the representation, we start out saying decimals are also fractions. Later we build a negative addition to the number line and add the opposites of fractions. Once we have a robust conception of the number line, inhabited by rational numbers, we want to talk about different ways of expressing those numbers: fractions, decimals, infinite decimals, expressions involving square root symbols and exponents. So we start to distinguish between fractions and decimals, not as numbers, but as forms for expressing numbers. We initially suppress their role as forms in order to gain a robust conception of number; once they are firmly attached to that conception we can distinguish between them.

They only way to do this without giving multiple meanings to the same words would be to invent new words and be consistent in their use. This harks back to the distinction between “numeral” and “number” in the New Math, which didn’t take hold.

Ways of thinking and ways of doing

/ Bill McCallum / 20 Comments

Somewhere back in days of Facebook fury about the Common Core there was a post from an outraged parent whose child had been marked wrong for something like this:
$$
6 \times 3 = 6 + 6 + 6 = 18.
$$
Apparently the child was supposed to do
$$
6 \times 3 = 3 + 3 + 3 + 3 + 3 +3 = 18
$$
because of this standard:

3.OA.A.1. Interpret products of whole numbers, e.g., interpret $5 \times 7$ as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as $5 \times 7$.

The parent had every right to be upset: a correct answer is a correct answer. Comments on the post correctly pointed out that, since multiplication is commutative, it shouldn’t matter in what order the calculation interpreted the product. But hang on, I hear you ask, doesn’t that contradict 3.OA.A.1, which clearly states that $6 \times 3$ should be interpreted as 6 groups of 3?

The fundamental problem here is a confusion between ways of thinking and ways of doing. 3.OA.A.1 proposes a way of thinking about $a \times b$, as $a$ groups of $b$. In other words, it proposes a definition of multiplication. It could have proposed the other definition: $a \times b$ is $b$ groups of $a$. The choice is arbitrary, so why make it? Well, there’s an interesting discovery to me made here: the two definitions are equivalent. That’s how you prove that multiplication is indeed commutative. It’s not obvious that $a$ groups of $b$ things each amounts to the same number of things as $b$ groups of $a$ things each. At least, not until you prove it, for example by arranging the things into an array:

You can see this as 3 groups of 6 by looking at the rows,

and as 6 groups of 3 things each by looking at the columns,

Since it’s the same number things no matter how you look at it, and using our definition of multiplication, we see that $3 \times 6 = 6 \times 3$. (We leave it as an exercise to the reader to generalize this proof.)

None of this dictates the way of doing $6 \times 3$, that is, the method of computing it. In fact, it expands the possibilities, including deciding to work with the more efficient $3 \times 6$, as this child did. The way of thinking does not constrain the way of doing. If you want to test whether a child understands 3.OA.A.1, you will have to come up with a different task than computation of a product. There are some good ideas from Student Achievement Partners here.

Misconceptions about Multiple Methods

/ Bill McCallum / 12 Comments

You may have noticed that I am back to publishing regular blog posts! My goal for now is a blog post every second Wednesday. I am now also trying to answer forum questions promptly. I want to thank the readers who took up the slack for the last year and a half in answering questions in the forums. In particular, I’d like to call out abieniek, Alexei Kassymov, and Lane Walker, whose answers were always spot on.

Now to the topic of this post. There has been a lot of talk since the standards came out about what they say about multiple methods for arithmetic operations, and I’d like to clear up a couple of points.

First, the standards do encourage that students have access to multiple methods as they learn to add, subtract, multiply and divide. But this does not mean that you have to solve every problem in multiple ways. Having different methods available is like having different means of transportation available to get to work; flexibility is good, but it doesn’t mean you have to go to school by car, then by bus, then walk, then bike—every single day! The point of having multiple methods available is to encourage students to think strategically about what might be the best method for a given problem, not force them to solve every problem four times.

Second, the different methods are not unrelated; they form a progression, with the ultimate goal being the standard algorithm. For example, when students are first learning to multiply two digit numbers, they might use a rectangle to represent a product such as $42 \times 71$.

This shows the fundamental role of the distributive property in multiplying multi-digit numbers. You have to multiply each base ten component into each other one. Indeed, the same rectangle representation provides a visual proof of the distributive property itself.

At some later point students might just start writing down all the partial products, without using the rectangle to derive them.

Note the correspondence between the rectangle method and the partial product method, indicated by the colors. The first row of the rectangle and shows all the products by the 2 in 42 (in red); the second row shows all the products by the 40 (in blue). The products in the partial product method are grouped in the same way. There are many ways you can order the partial products, but if you group them as I have here, going from right to left in each two-digit number, as in the standard algorithm, you make an amazing discovery: you can add up all the partial products in each group (blue group or red group) in your head as you go along. That’s because, in each case, adding the 2 to the 140 or the 40 to the 2800, there are enough zeroes in the second addend to accommodate the first, so it is easy to write down the sum right away, without writing the addends separately.

OK, so it’s not always quite this easy, because every now and then you will have to keep in mind a bundled unit from the previous step (aka carrying), but you will never have to remember that for more than one step at a time, because each bundled unit gets used up at the next step. So if you invent a notation for remembering the bundled unit (what we used to call “little 1 in the corner” when I was growing up) then you can still avoid writing down all the partial products, and just compute the sum within each group as you go along. You have just created the standard algorithm.

The different methods are not isolated different ways of doing the same thing; they are steps towards fluency with the standard algorithm, fluency that is not fragile because it is supported by understanding.

Curricular Coherence no. 4: Coherence of Practice

/ Al Cuoco / Leave a comment

In this final post about curricular coherence, I’m pinch-hitting for Bill, who is busy reorganizing his wine cellar.  This time, we talk about coherence of mathematical practice.

We value coherence of content because we believe that a coherently arranged curriculum makes it possible for a student to see the subject as a whole, to understand the logical connections and deep structures, and to use that understanding for more efficient problem-solving and better retention of knowledge and procedures. But making it possible does not make it probable. The way students do mathematics, their mathematical practice, may have an effect on their ability to take advantage of a coherent curriculum. The CCSSM describes eight aspects of the complex construct of mathematical practice. Here we focus on two aspects, using structure (MP7) and abstraction (MP8).

Structure in arithmetic and algebraic expressions reveals what might be called “hidden meaning.” For example, writing $x^2-6x-7$ as $(x-3)^2-16$ reveals that, for real values of $x$, the expression assumes values greater than or equal to $-16$ (and it assumes that value only when $x=3$). Writing it as $(x-7)(x+1)$ highlights the values of $x$ that make the expression 0.

Treating pieces of expressions as a single “chunk” can simplify calculations; seeing that $4x^2-8x+3$ can be written as $(2x)^2-4(2x)+3$ helps one obtain the factorization from the (easier) factorization of $z^2-4z+3.$ This example can be generalized to encompass all polynomial expressions, providing students with a general purpose tool that can be used to transform a general polynomial into one with leading coefficient~1. It amounts to a change of variable in order to hide complexity, a practice that is useful all over mathematics.

Hidden meaning in geometric figures often involves the creation of auxiliary lines not originally part of a given figure. Two classic examples are the construction of a line through a vertex of a triangle parallel to the opposite side as a way to see that the angle measures of a triangle add to $180^\circ$ and the introduction of a symmetry line in an isosceles triangle to see that the base angles are congruent. Another kind of hidden structure makes use of the invariance of area when it is calculated in more than one way—finding the length of the altitude to the hypotenuse of a right triangle, given the lengths of its legs, for example.

A final example of using structure is in the view that students form of the base ten notational system. The compactness and regularity of this system make it useful for efficient computation and estimation. But in that compactness there is also the danger of superficial, and therefore fragile, grasp of procedures. The Number and Operations in Base Ten domain in CCSSM lays out a progression designed to help students learn to see the decimal expansion of a rational number as, in advanced language, a linear combination of powers of 10 with coefficients taken from integers between 0 and 9 helps. Similarly, viewing a polynomial in $x$ as a linear combination of powers of $x$ can lead to an understanding of polynomial algebra as a system in its own right. Writing $3x^2-7x + 5$ “in base $(x-2)$” as
$$
3(x-2)^2+5(x-2) + 3
$$
reveals another kind of hidden meaning in the expression.

Another theme that runs throughout a coherent curriculum is a cross-grade emphasis that helps students develop and use the many faces of abstraction. One of the most important uses of abstraction is captured in the CCSSM Standard for Mathematical Practice no.~8 (MP8), “Look for and express regularity in repeated reasoning.” It asks students to abstract a process from several instances of that process in a way that doesn’t refer to the inputs to any particular instance. Describing that process in precise algebraic language allows one to create general algorithms, equations, expressions, and functions. This practice can bring coherence to many seemingly different areas of the curriculum that often cause students difficulty.

The description of MP8 in CCSSM gives the following example:

By paying attention to the calculation of slope as they repeatedly check whether points are on the line through $(1, 2)$ with slope 3, middle school students might abstract the equation $\frac{y – 2}{x – 1} = 3$.

Helping students develop the habit of testing several numerical points to see if they are on the line and then looking for and expressing the “rhythm” in their calculations gives them a way to find the equation of a line between two points without leaning on formulas (“point slope form,” for example), and, more importantly, it gives them a general purpose tool for finding Cartesian equations of geometric objects, given some defining geometric conditions.

As another example, consider the task of building an equation. Teachers know that building is much harder for students than checking. The same practice of abstracting from numerical examples is useful here, too. For example, consider the stylized story problem:

Emilio drives from Tucson to Phoenix at an an average speed of 60MPH and returns at an average speed of 50MPH. If the total time on the road is 4.4 hours, how far is Tucson from Phoenix?

The practice of abstracting regularity from repeated actions can be used to build an equation whose solution is the answer to the problem: One takes several guesses (for the distance) and checks them, focusing on the steps that are common to each of the checks. The goal isn’t to stumble on (or approximate) an answer by “guess and check;” the goal is to come up with a general “guess checker” expressed as an algebraic equation:
$$
\frac {\text{guess}}{60} + \frac {\text{guess}}{50}= 4.4
$$

These two examples seem quite different, but coherence comes from the fact that exactly the same mathematical practice is used to find an algebraic equation whose solution solves the problem.

Curricular Coherence Part 3: Using Deep Structures to Make Connections

/ Bill McCallum / Leave a comment

In this post I’d like to describe the third aspect of coherent content that Al Cuoco and I have been thinking about. In my fourth and final post on this subject I will talk about coherence of practice.

A difficult question in designing a curriculum is to decide which topics go together. The logical and evolutionary considerations described in my previous two posts help, in that they provide guidance on the ordering of topics. But that still leaves many decisions to be made. My goal this post is to show some examples of how deep structures can guide these decisions. (See my previous post for what we mean by a deep structure.)

CCSSM in 6th grade has the following standard about percents in the Ratio and Proportional Reasoning domain:

6.RP.A.3c. Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.

One approach to implementing this standard in a curriculum would be to have a section on percents that covers everything in the standard. But there is another possibility which attends to the difference between the parts of this sentence before and after the semicolon. The first part introduces the concept of percent. The second half involves solving problems that are tantamount to solving the equation $px = q$, where $p$ and $q$ are constants. This is related to a standard in the Expressions and Equations domain:

6.EE.B.7. Solve real-world and mathematical problems by writing and solving equations of the form $x + p = q$ and $px = q$ for cases in which $p$, $q$ and $x$ are all non-negative rational numbers.

Thus another possibility might be to split the treatment of the percent standard into two places in the curriculum, with the introduction to percents occurring as a type of rate, in the section where ratios and rates are studied, and percent problems occurring in the section where solving equations is studied. If percents are regarded as a deep structure, one might choose the first arrangement; if rates and equations are regarded as deep structures, then one might choose the second. The second approach is the one we have taken in our soon-to-be-released middle school curriculum.

Another example of a deep structure is the profound connection between geometry and algebra. Imagine a 12 by 16 rectangle. Experiments with geometry software suggest that a square of side 14 maximizes area for the perimeter of this rectangle. If this is so, it should be possible to dissect the rectangle and fit the pieces into the square with something left over.

Trying several other rectangles of perimeter 56, a regularity emerges. Expressing this regularity in precise language leads to an algebraic identity that captures the dissection. Using an $a\times b$ rectangle, one has
$$
\label{eqagm} \left(\frac{a+b} 2\right)^2
-\left(\frac{a-b} 2\right)^2=ab
$$
This identity, inspired by geometric reasoning, can, of course, be verified in an algebra course. But its roots in geometry give it some extra meaning. And, it can be used to show how far off the rectangle is from the square.

Rather than separating the parts of this connection into two chapters or lessons, a coherent curriculum could use one story to develop both the necessary algebra and geometry, making it explicit that the main point is the connectivity of the ideas.

Curricular Coherence Part 2: Evolution from Particulars to Deep Structures

/ Bill McCallum / 2 Comments

In my previous post on curricular coherence I talked about how the principle of logical sequencing can determine the ordering of a set of topics. Since time is one-dimensional, and curriculum occurs over time, some principle for ordering is necessary. However, mathematics is not a linearly ordered set of topics; it is better viewed as a network. In this post I’d like to talk about deep structures. A deep structure is, roughly speaking, a node in the network of mathematical knowledge with many connections. Of course, this is not a precise definition; the organization of the subject into a network is to a certain extent a matter of judgment and preference, although some connections are dictated by the principle of logical sequencing. However, this will serve for a start in describing the principle of evolution from particulars to deep structures.

I’ll talk about two ways in which the such evolution occurs: extension and encapsulation. Extension is a process by which a particular principle is repeatedly applied to ever broader systems, thus revealing its nature as a deep structure. Encapsulation is a process by which a related array of concepts and skills becomes encapsulated into a single compound concept or skill.

Extension is exemplified in the way that arithmetic with whole numbers is extended to fractions, integers, and rational numbers through a program of preserving the properties of operations. The fact that $(-3)\times (-5)$ is 15 is a definition, rather than a theorem—it has to be that way if we want arithmetic with integers to obey the distributive property. The properties of operations start from observation of particular instances, and evolve into powerful deeper structures under-girding the number system.

A good example of encapsulation is the development of fractions. The standard 3.NF.A.1 expects students to “Understand a fraction $1/b$ as the quantity formed by 1 part when a whole is partitioned into $b$ equal parts; understand a fraction $a/b$ as the quantity formed by $a$ parts of size $1/b$” and 3.NF.A.2 expects students to use this understanding to represent fractions on a number line. These two standards encapsulate many prior ideas and activities: dividing a physical object into halves or thirds; recognizing a geometric figure as a fraction of a larger figure representing the whole; moving from area representations to linear measurement representations; understanding the number line as marked off in unit lengths; subdividing those lengths into $n$ equal parts and thinking of those parts as a new sort of unit, an $n$th, and measuring out distances in those new units; correlating all these activities to the numerator and the denominator of the fraction.

Encapsulation builds coherence by tying what were previously disparate ideas and actions into a tightly connected structured bundle which becomes viewed as an object in its own right.

Proportional relationships

An important type of encapsulation is the evolution of representations. Mature representations are a form of encapsulation, and should be developed through a sequence of intermediate representations whose structural features preserve information about the object being represented. In early grades students might start with pictorial representations; but even then the picture should be more than a picture: it should carry information about the situation. Over time, such pictures evolve into more abstract diagrammatic representations, and eventually these diagrams are replaced by even more abstract representations such as tables and equations. The figure shows such an evolution for representations of proportional relationships in middle school. That final equation $y=kx$ is very dense with meaning, or at least it should be so for students. By the way, this is the sequence of representations for proportional relationships that we use in our new middle school curriculum coming out in July.

What Does It Mean for a Curriculum to Be Coherent?

/ Bill McCallum / 3 Comments

Al Cuoco and I have been thinking about this question and have developed some ideas. I want to write about the first and most obvious one today, the principle of logical sequencing. I’ll write about others in the weeks to come.

Remember the distinction between standards and curriculum. While standards might remain fixed—a mountain we aim to help our students climb—different curricula designed to achieve those standards might make different choices about how to get there. Whatever the choices, a coherent curriculum, focused on how to get students up the mountain, would make sense of the journey and single out key landmarks and stretches of trail—a long path through the woods, or a steep climb up a ridge.

By the same token, mathematics has its landscape. CCSSM pays attention to this landscape by laying out pathways, or progressions, that span across grade levels and between topics, so that a third grade teacher understands why she is teaching a particular topic, because it will help students with some other topic in the next grade and build on what they already know.

This leads us to the first property of a coherent curriculum: it makes clear a logical sequence of mathematical concepts.

Consider, for example, the concepts of similarity and congruence. It is quite common in school curricula for similarity to be introduced before congruence. This comes out of an informal notion of similarity as meaning “same shape” and congruence as meaning “same shape and same size.” However, the fact that the informal phrase for similarity is a part of the informal phrase for congruence is deceptive about the mathematical precedence of the concepts. For what does it mean for two shapes to be the same shape (that is, to be similar)? It means that you can scale one of them so that the resulting shape is both the same size and the same shape as the other (that is, congruent). Thus the concept of similarity depends on the concept of congruence, not the other way around. This suggests that the latter should be introduced first.

This is not to say you can never teach topics out of order; after all, it is a common narrative device to start a story at the end and then go back to the beginning, and it is reasonable to suppose that a corresponding pedagogical device might be useful in certain situations. But the curriculum should be designed so that the learner is made aware of the prolepsis. (Really, I just wrote this blog post so I could use that word.)

Although the progressions help identify the logical sequencing of topics, there is more work to do on that when you are writing curriculum. For example, the standards separate the domain of Number and Operations in Base Ten and the domain of Operations and Algebraic Thinking, in order to clearly identify these two important threads leading to algebra. But these two threads are logically interwoven, and it would not make sense to teach all the NBT standards in a grade level separately from all the OA standards.

In the next few blog posts, I will talk about three other aspects of coherent curriculum: the evolution from particulars to deeper structures, using deep structures to make connections between topics, and coherence of mathematical practice.