In my last post I wrote about the following standard, and mentioned that I could write a whole blog post about the first comma.

8.F.A.3. Interpret the equation $y = mx + b$ as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function $A = s^2$ giving the area of a square as a function of its side length is not linear because its graph contains the points $(1,1)$, $(2,4)$ and $(3,9)$, which are not on a straight line.

The comma indicates that the clause “whose graph is a straight line” is nonessential for identifying the noun phrase “linear function.” It turns the clause into an extra piece of information: “and by the way, did you know that the graph of a linear function is a straight line?” This fact is often presented as obvious; after all, if you draw the graph or produce it using a graphing utility, it certainly looks like a straight line.

When I’ve asked prospective teachers why this is so, I’ve gotten answers that look something like this:

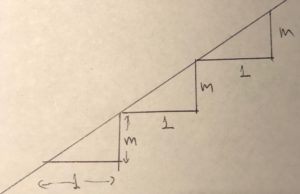
We know that a linear function has a constant rate of change, $m$. If you go across by 1 on the graph you always go up by $m$, like this:

So the graph is like a staircase. It always goes up in steps of the same size, so it’s a straight line.

This is fine as far as it goes. It identifies the defining property of a linear function—that it has a constant rate of change—and relates that property to a geometric feature of the graph. But it’s a “Here, Look!” proof. In the end it is showing that something is true rather than showing why it is true. Which is to say that it’s not a proof.

Still, the move to a geometric property of linear functions is a move in the right direction, because it focuses our minds on the essential concept. We all know that any two points lie on a line, but three points might not. What is it about three points on the graph of a linear function that implies they must lie on a straight line?

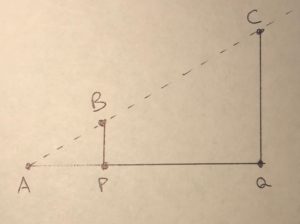
Line from $A$ to $B$ to $C$ is dotted because we don’t know it’s a line yet

Because a linear function has a constant rate of change, the slope between any two of the three points $A$, $B$, and $C$ is the same. So $|BP|/|AP| = |CQ|/|AQ|$, which means there is a scale factor $k =|AQ|/|AP| = |CQ|/|BP|$ so that a dilation with center $A$ and scale factor $k$ takes $P$ to $Q$, and take the vertical line segment $BP$ to a vertical line segment based at $Q$ with the same length as $CQ$. Which means it must take $B$ to $C$.

But (drumroll) this means that there is a dilation with center $A$ that takes $B$ to $C$. Dilations always take points on a ray from the center to other points on the same ray. So $A$, $B$, and $C$ lie on the same line.

I don’t really expect students to get all of this, at least not right away. I’d be happy if they understood that there is a geometric fact at play here; that seeing is not always believing.