We ended the previous post with a bit of a cliffhanger, with two possible diagrams to represent $1\frac34 \div \frac12$:
The first of these diagrams is more familiar to students because it reflects their past work, but the second is more productive for understanding “dividing by a unit fraction is the same as multiplying by its reciprocal.”
Why is the first one more familiar? In grades 3 and 4, students study both the “how many in each (or one) group?” and “how many groups?” interpretations for division with whole numbers (see our last blog post for examples). In grade 5, they study dividing whole numbers by unit fractions and unit fractions by whole numbers. But, as we mentioned in that post, in grade 5 the “how many groups?” interpretation is easier when dividing whole numbers by unit fractions because students do not have to worry about fractions of a group. Going from $3 \div \frac12$ to $1\frac34 \div \frac12$ using this interpretation feels fairly natural:
The main intellectual work here is seeing that $\frac14$ cup is $\frac12$ of a container, but because the structure of the problem is the same and that structure can be easily seen in the diagrams, students can focus on that one new twist. The transition also helps students see that “how many groups” questions can be asked and answered when the numbers in the division are arbitrary fractions.
So the “how many groups” interpretation is useful for understanding important aspects of fraction division and has an important role in students’ learning trajectory. It enables students to see that dividing by $\frac12$ gives a result that is 2 times as great. But it doesn’t give much insight into why this should be the case when the dividend is not a whole number.
The “how much in each group” interpretation shows why. Here are diagrams using that interpretation showing $3 \div \frac12 = 2 \cdot 3$ and $1 \frac34 \div \frac12 = 2 \cdot 1 \frac34$.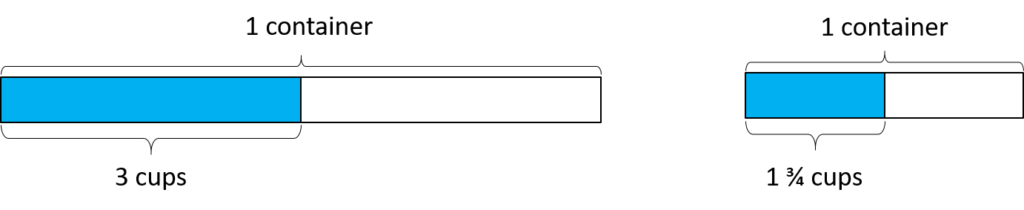 In fact, the structure of this context is so powerful, we can see why dividing any number by $\frac12$ would double that number: $$x \div \frac12 = 2 \cdot x = x \cdot \frac21$$
In fact, the structure of this context is so powerful, we can see why dividing any number by $\frac12$ would double that number: $$x \div \frac12 = 2 \cdot x = x \cdot \frac21$$
This is true for dividing by any unit fraction, for example $\frac15$: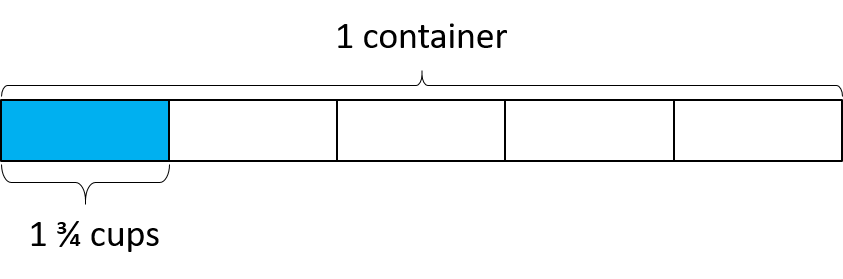 In the diagram above, we can see that $1\frac34$ is $\frac15$ of a container, so a full container is $1\frac34 \div \frac15$. Looking at the diagram, we can see why it must be that the full container is $5 \cdot 1 \frac34 = 1 \frac34 \cdot \frac51$.
In the diagram above, we can see that $1\frac34$ is $\frac15$ of a container, so a full container is $1\frac34 \div \frac15$. Looking at the diagram, we can see why it must be that the full container is $5 \cdot 1 \frac34 = 1 \frac34 \cdot \frac51$.
With a little more work to make sense of it, we can use this interpretation to see why we multiply by the reciprocal when we divide by any fraction, for example $\frac25$: In the diagram above, we can see that $1\frac34$ is $\frac25$ of a container, so a full container is $1\frac34 \div \frac25$. We can see in the diagram that $\frac12$ of $1\frac34$ is $\frac15$ of the container, so our first step is to multiply by $\frac12$: $$1\frac34 \cdot \frac12$$
In the diagram above, we can see that $1\frac34$ is $\frac25$ of a container, so a full container is $1\frac34 \div \frac25$. We can see in the diagram that $\frac12$ of $1\frac34$ is $\frac15$ of the container, so our first step is to multiply by $\frac12$: $$1\frac34 \cdot \frac12$$
Now, just as before, to find the full container, we multiply by 5:
$\left (1\frac34 \cdot \frac12 \right) \cdot 5 = 1\frac34 \cdot \frac52$
This shows that dividing by $\frac25$ is the same as multiplying by $\frac52$!
There is nothing special about these numbers, and a similar argument can be made for dividing any number by any fraction. Now students, instead of saying “ours is not to reason why, just invert and multiply,” can say “now I know the reason why, I’ll just invert and multiply.”
Next time: Beyond diagrams.


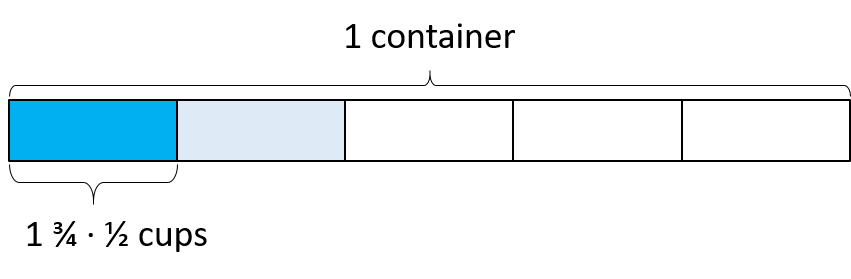
More amazing to me is that fraction division works without inverting and multiplying. 9/20 divided by 3/5 results in 3/4. Just divide the top lines and the bottom lines. Exploring this further will also explain why we invert and multiply.
Pingback: Diigo Links (weekly) | Mr. Gonzalez's Classroom