Here is an early draft of the progression for Number and Operations—Fractions. Unlike the other drafts I have posted, this one does not yet incorporate all the feedback we got from initial review, so more than usual I am interested in your comments. In particular I would like to know if it is too dense and needs more explanation, or if it is just right.
If you are reading it with Adobe Acrobat, you will need the latest version (10.1). If you are using a Mac, you can also use the native Mac pdf reader Preview, or the open source pdf reader Skim.
We hope to get drafts of the remaining K–8 progressions out soon; thank you for your patience.
[File updated 2/5/12 to fix printing problems.]
[File updated 9/19/13 with corrections.]
[31 July 2012] This thread is now closed. Please ask questions here.
Dr. McCallum,
I am a secondary mathematics director for a school system in Maryland. We have 14 middle schools and ten high schools. I am presenting reading the PARCC Model Content Frameworks–which (frequently) alerted me in your blogs, among other resources. I look forward to reading your blog and (perhaps) becoming a regular contributor of comments.
Thank you for your work with the standards and the progressions.
Peter Cincotta
Dear Dr. McCallum,
I am a local tutor in Austin Texas, who majored with a Masters with a concentration in Curriculum and Instruction from UT several years ago. I frequently find myself explaining math concepts to students of differing levels of proficiency and rigor. I deal with students and learners who have various learning styles and proficiencies. How well this curriculum incorporates scaffolding and prior learning of students….have studies been done on the level of absorption of students as they advance from one grade to the next?
I am interested primarily to see a nuts-and-bolts version of curriculum which principals and teachers will eventually use. It is fascinating to see it designed like this. The second and third grade work is spot-on, and it should prepare them for sixth grade work with ratios and proportions. Although the curriculum hasn’t changed much since the years I was in school, presenting the fractions, particularly in the grey box visualizations is nice and concise. How each teacher then communicates the material is to each his or her own.
How can I join a community in actually constructing the framework of the curriculum that principals, teachers, and students will actually use? Are there resources of such conciseness such as those grey box grids that I may use freely with those that I tutor? If I may be of help, please contact me by direct message at twitter at username atxlocaltutor where I am following NASBE.
Sincerely,
Yen-Hong Tran
[phone number deleted]
First, there’s a difference between standards and curriculum, and curricula based on the Common Core are just now being developed. However, in developing the standards we drew on the expertise of researchers who have looked at the sequencing in elementary grades, and also aligned with with standards of high achieving countries.
As for you question about community, states that have adopted the Common Core are actively developing frameworks, but Texas is not one of them, I’m afraid!
Dr. McCallum,
The question has arisen among math teachers inquiring what is meant by the tern “traditional algorithm” in the elementary math standards. We have had some conflicting information and ideas about this, mostly presented by a publisher. Could you please lend some clarity?
Sally M. Mascia
Take a look at the Number and Operations in Base Ten progression, at http://commoncoretools.me/2011/04/06/draft-of-progression-on-number-and-operations-in-base-ten/, and see if it answers your questions.. The Standards strike a balance between having students work with various algorithms that might initially help them understand the structure of the base ten system (such as the expanded algorithm for multiplication) and having them become fluent in the standard algorithm. If there are specific conflicts that your publisher has raised, I’d be happy to discuss them.
First of all, THANK YOU!!
The fact that the common core standards really does a fantastic job with one of the most challenging/misunderstood concepts is fabulous. This progression adds additional context.
The biggest mind-shift for me that was illustrated so clearly in the progression is the building from a unit fraction. The fact that one just sums the unit fractions, regardless of whether that “one” threshold is crossed- make so much more sense to NOT make the distinction early one between “proper” and “improper” fractions. The other shift for me in my teaching will be focusing on multiplication as repetition (by focusing on whole numbers), just as with whole numbers until students truly can start to notice patterns and extend thinking in 5th grade. I have always done repetition as one case, but moved pretty quickly into part of a whole as another case. The standards and the progression by extension, are well thought out in this area.
There are two questions that I still have (granted, I have only read this progression twice)
1. Fraction equivalence. Are students really not expected to multiply by a fractional whole until 5th grade? Seems so “modeled” and not explicitly mentioned until 5th.
2. Division of fractions. I have looked into tape model (Singapore modeling) for this concept, especially where as 5th grade only does division of unit fractions and wholes. Are you in support of these modeling techniques? The most illustrative I found was this: http://www.youtube.com/user/mathplayground#p/u/8/_11SEY-P_h0
Jen Spencer
Formerly middle school math teacher
currently part time coordinator for a math collaboration for 4th and 5th grade
1. I’m not completely sure I understand this question, but here is a try. The concept of fraction equivalence starts in Grade 3, with the simple idea of being able to name the same number in two different ways, e.g. 1/2 and 2/4. It is developed more fully in Grade 4, where students reason directly with visual fraction models to see that taking, say, 3 times as many copies of a unit fraction one-third the size gives you the same number. In Grade 4 students have not yet completed general fraction multiplication, they are just multiplying fractions by whole numbers. Once they get to Grade 5 and have general fraction multiplication, they can see fraction equivalence as a case of that, (a/b) x (n/n) = an/bn. In practice, many students will see that pattern earlier (and teachers will point it out), and use it as a way of remembering who fraction equivalence work. There’s no great harm in that in my opinion. But you also want students to have deeper understanding of fraction equivalence in terms of the actual size of numbers.
2. Yes, this sort of model certainly fits with the standards. But when I looked at the video I was disappointed that the instructor didn’t make a more direct connection between the moment in where she subdivided the 6ths into 2 pieces, and the moment where she used the formula and multiplied the denominators. Because she subdivided first just the middle block of the 5 sixths, and then all the rest (“to make it clearer”), she never got to say: “look, I have to subdivide all this sixths into 2 pieces in order to take half of the 5 sixths, and notice that means I now have 12 = 2 x 6 pieces.” I thought that was a missed opportunity to use the diagram to explain why you multiply the denominators.
Thank you for your thorough response.
1. Here is my take away from your response- hopefully I have characterized appropriately: Students identify common equivalence in 3rd, generate common equivalence through visual models in 4th, extend concept of equivalence by identifying pattern of multiplying by a whole in 5th.
2. I completely agree with the video- definitely a bit of a cop out to go through all of the thorough explanation and then give a “to make it clearer” instead of just making it a given that you have to divide EACH of the parts in two. I do plan on using some of the videos for training purposes so will be on the look out for those opportunities.
That’s basically correct, although I would say that in Grade 4 the central method is reasoning from the understanding of a fraction as being built up from unit fractions. In practice, this will no doubt be supported using visual models, but there might be simple cases where a student can see directly that, for example 2/3 = 4/6 by reasoning numerically.
A little more about tape diagrams. Some different forms are illustrated in the OA Progression for K–5 here: http://commoncoretools.me/2011/05/29/complete-draft-progression-for-cc-and-oa/. You can get to most examples by searching the pdf for “tape.”
So, their use in the progressions might help to illustrate thinking about building on students’ prior knowledge. Students can first use tape diagrams to represent addition and subtraction of whole numbers, and later of fractions. They can make similar use for multiplication and division. The diagrams help to illustrate aspects of the operations, for example, the connection between addition and subtraction.
Bill,
Thank you for posting the draft progression on fractions. Even though it is still a draft, the document cleared (I think) a couple of questions I had. Of course, it raised some other questions/issues, but I suppose that’s the whole point of publishing a draft for people’s comments.
P. 1 There is a statement in the document, “In Grade 4, this is extended to include wholes that are collections of objects.” So, does this mean that “fraction of sets” is not to be discussed until Grade 4? I will completely support such a decision, but I think it may have to be stated more explicitly.
p. 1 I really appreciate the emphasis on unit fractions and how (non-unit) fractions are composed of unit fractions. Reading the statement, “there is no need to introduce ‘proper fractions’ and ‘improper fractions’ initially; 5/3 is the quantity you get by combining 5 parts together when the whole is divided into 3 equal parts” made me realize that the CCSS does not restrict fractions in Grade 3 to be those that are less than 1. While I was reading the CCSS itself, I assumed that in Grade 3, students will only consider fractions less than 1. Of course, that makes it rather strange to think about whole numbers as fractions (3.NF.3.c). When I went back to the CCSS, I saw that, in the grade 3 summary page, there is the statement, “Students are able to use fractions to represent numbers equal to, less than, and greater than one.” Perhaps this needs to be emphasized a bit more in the progression document.
Speaking on the “range of fractions,” in the CCSS (p. 24) there is a footnote saying “Grade 3 expectations in this domain are limited to fractions with denominators 2, 3, 4, 6, and 8.” I really don’t see the point of this restriction. In fact, in the summary paragraph, they say that children should understand that “1/3 of a ribbon is longer than 1/5 of the same ribbon.” I can see the restriction if we are continuing with partitioning geometric shapes, but I think students should be able to deal with unit fractions with any denominator. I can understand some restrictions in Grade 5 when adding fractions with unlike denominators.
Speaking of partitioning geometric shapes, the draft document says (p. 2), “Initially, students can use an intuitive notion of congruence (“same size and same shape”) to explain why the parts are equal…” I really don’t see the point of having students partition geometric shapes in Grades 1 and 2. In fact, I think those activities promote some misconceptions in students because they have yet to learn the concept of area as a measurable attribute. Since they don’t have a way of dealing with area to establish equality of parts, they will have to rely on either the informal sense of congruence, as the draft document says, or simply counting. I have seen upper elementary students (and sometimes even adults) who think that a whole must be partitioned into congruent parts to show fractions – so if a square is cut in half by a vertical line in the middle, then one side (a rectangle) is cut by a diagonal and the other by a horizontal segment, they would not say that one part is 1/4 of the square because the parts are not the same shape. Another misconception I have seen is that there must be 4 parts, for example, to show 1/4. So, if a quadrant of a square is shaded but the rest of the square is not partitioned, they would say it does not show 1/4 because there aren’t 4 parts. Another one is that students would say that all parts must be equal. So, if a quadrant of a square is shaded, but the remaining part is divided into 3 unequal size pieces, they would say that the shaded part is not 1/4 because the parts are not equal. I think these misconceptions result in part because we use area model to teach fractions when students have yet to develop a solid understanding of area measurement.
p.2 The number line shown has the line extending to the left of 0. I wonder if that is appropriate for Grade 3 students.
p. 2 The document says, “The number line reinforces the analogy between fractions and whole numbers.” I think this is a very important point – particularly with the emphasis in the CCSS on understanding fractions as numbers. In some ways, we want students to realize that fractions are numbers because they can be represented on a “number line” just like whole numbers can. In the Japanese curriculum, they would also include some simple addition/subtraction in the introductory unit for the same purpose – because we can add 2/5 and 1/5, like whole numbers, they must be numbers.
p. 4 Re. representing whole numbers as fractions. I always wondered why the CCSS (3.NF.3.c) seems to emphasize so much about whole numbers as fractions with the denominator of 1. At the time of introducing fractions, the notion of 1 as the denominator is so counter intuitive to children. I don’t see the idea serving any purpose at this stage. In fact, the only reason the idea of 1 as the denominator is discussed in traditional textbooks is so that they can multiply/divide whole numbers with fractions.
p. 6 I was very happy to see the statement about “multiplying by 1” is an inappropriate justification for generating equivalent fractions in Grade 4.
p. 7 I think it is important for the document to emphasize that “multiplying by a whole number” means, for example, “5 x 1/3,” but not “1/3 x 5.” Too often, teachers don’t distinguish the multiplier and the multiplicand, so they would think both of these are “multiplying by a whole number.”
p.8 I really do not think money is a good model to teach decimal numbers. Although we use notation that is similar to decimal numbers, money has 2 units, and the “dot” simply separate the two units. I have yet to see anyone who think 30 cents as 0.3 (nor 0.30) dollars. It is simply “thirty” cents. I don’t see why we cannot deal with “0.1” as a different representation of “one of 10 equal parts of 1,” which can also be represented as 1/10. Just as 3/10 means the collection of 3 1/10’s, 0.3 means the collection of 3 0.1’s. The idea of seeing 2.7 as 2 ones and 7 0.1’s, or 27 0.1’s, or even 270 0.01’s is simply an extension of the same idea with whole numbers: 13785 has 13 “thousands,” 137 “hundreds,” 1378 “tens,” etc. I’m not sure how much this idea is being emphasized in the NBT domain, but I think it is very important.
p. 10 The document says, “In Grade 4, students calculate sums of fractions with different denominators where one denominator is a divisor of the other,” but I don’t see that in Grade 4 standards. 4.NF.3.c says, “Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.”
p. 10 I appreciate the statement, “in fact, the effort of finding a least common denominator is a distraction from understanding algorithms for adding fractions.” But, I wondered if you should make more reference to subtraction in this section. Perhaps “addition/subtraction” is awkward, and readers will understand that what you are saying also apply to subtraction.
p. 11 I think you need a much more detailed elaboration on multiplication and division of fractions, in general.
I don’t know if children can naturally say,
“1/3 x 5 is one part when 5 is partitioned into 3 parts, so 4/3 x 5 Is 4 parts when 5 is partitioned into 3 parts.”
Perhaps you can also include a reasoning based on the property of operations, i.e., 4/3 x 5 = (4 x 1/3) x 5 = 4 x (1/3 x 5), too.
p. 11 In the example of 2/3 x 5/2, I don’t see why children would want to think about partitioning each of five 1/2’s into 3 parts, instead of partitioning 5/2 into 3 parts. Because the CCSS restricts the division in Grade 5 to unit fractions, this example is there, but I think it is so unnatural. Why not deal with dividing by whole numbers in Grade 5 and divide by fractions in Grade 6 – similar to the way multiplication is dealt with? For children, I think 4/5 divided by 2 is much easier than 1/5 divided by 2. Starting with something like 4/5 divided by 2, then children can think about the case where the numerator cannot be divided evenly by the divisor. Then, they can use the idea of equivalent fractions to deal with those cases.
I understand that you try to be consistent with the way multiplication expressions are written is (multiplier) x (multiplicand). Thus, you connect 5 divided by 3 with 1/3 x 5, not 5 x 1/3. When you discuss the way to generate equivalent fractions is to multiply both the numerator and denominator by the same number, it is expressed as a/b = nxa/nxb, instead of a/b = an/bn. In the discussion on multiplication by fractions, you have an example, (a/b) x q = a x q / b, splitting the fraction multiplier. I think all of these awkward situations can be avoided if we went with the convention (some might say that THE correct way) of writing (multiplicand) x (multiplier). After all, “division by a fraction is the same as multiplication by the reciprocal of the divisor” is more neatly expressed if we can say, “a/b div c/d = a/b x d/c” instead of “a/b div c/d = d/c x a/b.”
By the way, 5.NF.4.c says, “Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b.” But, I think you need a parentheses around q ÷ b to match the expression. a × q ÷ b means taking a part of q partitioned into b equal parts according to the order of operations.
OK, this has become way too long, so I will stop here.
Tad, thanks again for these useful detailed comments on the progression. As you observe, some of the issues you raise are issues with the standards themselves, but the progression can some times make amends for glitches in the standards. These comments will be very useful in making the final version of the progression.
Hello Bill,
I will not attempt to add to Tad’s comments but I would like to highlight the comment he makes related to awarding fraction names to partitions of shapes in Grades 1 and 2. That is, “In fact, I think those activities promote some misconceptions in students because they have yet to learn the concept of area as a measurable attribute.” I agree and often state it somewhat less elegantly as “you cannot use what you don’t have”. Students cannot use comparisons of area as a model of fractions before they can at least indirectly compare area. This is one of the basic ideas in the teaching of fractions that I have been attempting to communicate in New South Wales for a number of years.
Congratulations on the work to date on the progressions.
I mostly agree, but I think the words “half” and “quarter” are going to be used anyway, since kids learn them at home. They hear their parents say “I’ll only have half of that” when being served food, and observe the piece being cut into two congruent pieces (approximately congruent, in the case of food). So I think it’s worth having a working definition of very simple fractions based on division into congruent pieces. After all, when we start measuring area by counting how many unit squares fill a region, we are implicitly using the same notion.
I disagree. Students in first grade are introduced to halves when they are taught time. The standard in first grade is students tell time to the hour and half hour. In second grade students tell time to 5 minutes. Teachers can also focus on quarter of an hour.
I meant to say I disagree with Tad and Peter.
OK, I am a high school music teacher, not a math teacher. The new initiative in my school has every teacher no matter what the subject is they teach, choosing a common core standard to work on either from reading or mathematics. So the closest core standard I came to aligning to my subject is fractions, since when you teach rhythm, you teach about the names of the notes which are fractional names (whole, half, quarter, eighth, sixteenth, thirty-second notes & rests) & the time signatures (2/4, 3/4, 4/4, 6/8 etc). My students are having a hard time grasping these musical concepts because they didn’t grasp the basics of fractions back in grade three. I would be interested in someone showing me a lesson plan showing me a 3rd grade fractions concepts and then extending those concepts to the teaching of time signatures. Even though the notes have fractional type names, they have different beat value depending on which note represents. A quarter note can be worth 1 beat & an eighth note can be worth a 1/2 beat because the whole note equals 4 beats. That when the half note equals 1 (x/2 as in 2/2), or the eighth equals 1 (x/8) as in 6/8, all the other note values shift to align to which note is the beat note. My students get stuck on the name of the note also being the value of the note. Please help me to extend.
I’m not sure if I can offer any suggestion, but, as you mentioned, the naming of musical notes is almost circular – it is based on the fraction of one measure when a measure consists of 4 beats quarter notes.
One thing I felt I benefited from my earlier musical experiences is about equally partitioning a whole (not necessarily a whole note). Let’s say we are thinking of 4/4 signature. Clapping each beat (quarter notes), splitting each beat into 2 equal parts (eighth notes), 3 parts (triplets), 4 parts (16th notes), and how each note became actually shorter. That gave me the sense that the more you split a whole, the smaller each part became. I think there is a CCSS standard in Grade 3 that relates to this idea.
Later on, I learned the difference of 3/4 + 1/4 (dotted eighth and 16th) and 2/3 + 1/3 (tied first two notes of triplets and the third note) more physically as I played the trumpet in the band.
Good luck.
Saundra, thanks for your description. Although I don’t have wisdom to offer you, I now understand something that in 8 years of playing intuitively in the school band, I didn’t get: the translation of the time signatures.
Dr. McCallum,
As a follow up on Tad Watanabe’s post, I also appreciate the statement on p. 10 , “in fact, the effort of finding a least common denominator is a distraction from understanding algorithms for adding fractions.”
I would suggest something like the following be stated: “in fact, the effort of finding a least common denominator is a distraction. Finding a simple common denominator will focus the student on the concept and algorithms for adding fractions at this grade level. ”
Respectfully,
John Meinzen
Math Department Chair & IL Content Specialist to PARCC
Edwardsville, IL
We in the broad mathematical community are grateful for these discussions. A great need remains for the progression documents to be converted to tasks, activities, problems for teachers to work on collaboratively. This will help all gain familiarity and understanding into the meaning of each standard. Is anyone working on this?
Yes, the Illustrative Mathematics Project will be adding tasks to illustrate the standards soon, see illustrativemathematics.org
Bill,
This question is with regards to fractions/defimals as they related to 4.MD.2- “Use the four operations to solve word problems involving distances…including problems involving simple fractions or decimals…”
I have no problems solving problems involving simple fractions – foundations for this are solid in the NF standards at this grade. However, operations with decimals are absent from grade 4. (4.NF.5 through 7 deal with decimals, but not operations with them. Operations with decimals are introduced in 5.NBT.7 and the progression culminates at 6.NS.3.)
Are students supposed to learn to operate with decimals in grade 4 or not?
I guess one could argue that students can convert the decimals to fractions out of 10 or 100 (4.NF.6 going backwards), then perform the calculation on the fractions (4.NF.5), then convert the fractional answer back to a decimal (4.NF.6). But operations with decimals are clearly and explicitly addressed in grades 5 and 6, not grade 4.
Please advise.
As always, thanks for all of your guidance,
Brian
Brian, sorry for the delay in replying, I got a bit hijacked by work. The Common Core views (finite) decimals not as a separate sort of number, but as a way of writing particular sorts of fractions, namely fractions with denominator 10, 100 etc. You’ll notice in the footnote to the 4.NF domain that denominators of 10 and 100 are allowed for operations in Grade 4, so yes, operations include decimals, with the idea being that they would be viewed as fractions and this is a particular case of fraction addition and subtraction. This is essentially what you suggest at the end of your query, except that the idea is to avoid suggesting decimals are a different sort of number that needs to be converted to a fraction, but rather emphasize that, say, .3 is just another way of writing 3/10.
Bill,
As always, thank you for the clear reply. While I don’t have any problems with it, this one really surprised me because:
– In grade 5, there is a cluster titled, “Perform Operations with multi-digit whole numbers and with decimals to hundredths.”
– In grade 4, the related cluster is titled, “Understand decimal notation for fractions, and compare decimal fractions.”
While it is possible to make the connections as you describe, as a reader of the standards, it is not at all clear that I should be doing that. In fact, the two cluster titles listed above (and there related standards) lead me to conclude that decimal/fraction equivalences occur in grade 4 and decimal operations occur in grade 5.
To prevent others from coming to my incorrect conclusions, PLEASE clarify this, in explicit language, in the final version of the Progression for NF.
Sincerely,
Brian
Just as a followup, I would say that Brian’s initial reading is not too far off, in the sense the full-bore operations with decimal fractions don’t start until Grade 5, with the work in Grade 4 being preparatory. E.g., in Grade 4 students might add 0.31 + 0.06 by viewing them as fractions with denominator 100, whereas in Grade 5 you want them to just see that the sum is 0.37 because they know 31 + 6 = 37. The first understanding forms the basis for the second, of course, and some students will make the transition in Grade 4. But the Grade 4 standards do not require that. Point taken about clarifying all this in the progressions document.
I hope this gets a response, though I don’t think I’m in the right place. I am involved with a Math 5-8 workgroup and recently watched 4 secondary math teachers struggle with an answer to an example posed in the 7th grade probability section. After about 5 minutes of bouncing ideas back and forth, they got it. Then 6th grade teachers began saying (as they struggled with CCSS) “Just tell us what to teach and how!!” “AHA” momment. That’s the point!! As we struggle with it ourselves, we underatsnd the 8 habits of mind better, and I don’t believe anyone is going to tell us “how” to teach it! As we struggle with it, we’ll all figure it out together!
Thanks, I completely agree that teachers must lead the way. The standards were written to support teachers in that effort, and the progressions are designed to flesh out the standards so that 6th grade teachers can see where the math they teach is leading to in 7th grade.
By the way, the Statistics and Probability Progression will be ready and posted on this website soon.
Thanks, Bill (and the CCMS team) for leading the way on this! I am so excited about doing something for students regarding mathematics education that I believe (regardless what happens after) is the right thing to do for our students. I heard Jason Zimba say that the CCSS were the biggest gift to math teachers in years. Thanks for the gift to our students too!!!
Can I ask one more question that is related, but about another author’s contributions to the teaching of the CCSS? I am certain that you have heard of Hung-Hsi Wu. He published an article two years ago in the American Teacher about the sophistication in elementary mathematics. Now he’s published another article about CCSS, “Phoenix Rising”, in the same magazine. I find myself agreeing with much of what he says, and reading a lot of what he’s published in the last 2 years. Wondering whether the CCSS Committee has an official position on his content regarding math education/professional development? Is there anyone else (besides the obvious – McCallum, Zimba, Daro, etc.) that I should be reading?
Well, I think I’ve discovered my own answer about Dr. Wu since he is one of the writers for the progression documents! Discovered this when I visited the U of A site!
I, too, have read “Phoenix Rising” by Dr. Wu. And then I sent it to all of my HS and MS mathematics department chairs to read. That article correctly describes–in my view–exactly what we want mathematics education to be. I am now reading Dr. Wu’s “article” on the teaching of Fractions grade-by-grade as the CCSS intends. I put “article” in quotes, because it is more like a short book (less than 100 pages). Again, this is what we want mathematics education to be.
I have finished that article and am now reading “The Math K-12 Teachers Should Know”, also by Wu. Most of this article focuses on what is needed as far as PD is concerned. Certainly has given me much to ponder.
Dear Dr. McCallum,
I am at a workshop in Billings, MT. Fabulous information! I would like to suggest an addition to the wording on “precision”. I would like to suggest “accuracy” be added to “precision”. Measurement can be very precise without being accuracy. I believe both properties are important to achieve. Thank you so much for the incredible volume of work in providing an outstanding resource to bring our states back together again in educations!
Sincerely,
Liz Madden
8th Grade Physical Science
Will James Middle School
Billings, MT 59102
maddenl@billingsschools.org
I agree that there’s a different between precision and accuracy. Attending to precision is being clear in your use of mathematical language and ideas; using words precisely, stating precisely what you know (including giving clear error bounds on a possibly “inaccurate” measurement), and so on.
I am wondering if there is any type of matrix for multiplying and dividing of fractions, similar to what the Massachusetts CCSS has on page 183 and 184 of this document. These pages show examples of questions for situations when either the groups are known or the groups are unknown, as well as comparison problems. I have been trying to create a matrix for multiplication/division of whole numbers divided by fractions, fractions divided by fractions, fractions divided by whole number examples that would fall into the partitive and measurement categories. Have you created anything like this or are you intending to include anything like this in the progressions? It might be best located in the 6th grade.
I am a math support and special educator in the Boston public school system.
Three suggestions…. First, What Works Clearinghouse (USDoE) has a document about teaching fraction /operations in grades 3-6. Although this document was created in 2008 (?) or thereabout, it is amazing how much it sounds like 2 other great resources for this content. One is John Van de Walle’s work on teaching student-centered mathematics (comes in 2 different grade level strands, 1-4 and 5-8 I think). The other source is Hung Hsi Wu’s work with teaching fractions, available on his website through Cal Berkeley.
Wu’s work is one of my two key resources in teaching fractions to my 5th graders. The other is the work here, by Bill McCallum. Thanks for providing another source of perspective for this important area. Fractions can be a “tipping point” for students. This country’s history in fraction instruction leaves many behind. Let’s hope that PD is available soon on these more intuitive and more grounded approaches.
Dr. McCallum,
I read your progression on fractions with great interest. I have a question. It seems as though, in other posts, that I’ve seen you refer to K-8 progressions. However, the fractions progression ends with grade 5. Can you tell me if, in the revision of the draft, you intend to include anything beyond that grade level? There is some in 6th.
Thanks
We will eventually come out with a progression for The Number System domain, Grades 6-8, and that will include the fraction material in Grade 6.
Hello Bill
One final comment in response to your statement “So I think it’s worth having a working definition of very simple fractions based on division into congruent pieces.” The way I read CCSS for Grade 3, developing an understanding of area, developing understanding of fractions, especially unit fractions; and describing and analyzing two-dimensional shapes are 3 of the 4 focus areas in Grade 3. I have no concerns about students using the terms halves and quarters (or fourths) in context. My concern is about the basis of the student’s understanding that the pieces are equal (congruent). The area model of fractions relies upon fractions as comparisons of area. In Grade 3 “Students recognize area as an attribute of two-dimensional regions. They measure the area of a shape by finding the total number of same-size units of area required to cover the shape without gaps or overlaps…”.
To use the area model of fractions students must:
Know what area is,
Identify the area of the part,
Identify the area of the whole, and
Compare the two areas by direct or indirect measurement.
This is not a problem when students know enough about area to be able to do this.
That is, the concern is not about the introduction of one half or one quarter but the use of the area model to teach fractions when students have yet to develop a solid understanding of area measurement.
Interesting. I wonder about the area model myself. It is a ubiquitous representation of fractions for kids…
I’m thinking about this (and all fractions instruction these days, frankly) in the context of the excellent book Extending Children’s Mathematics by Empson & Levi (2011). If you’ve not read it yet, one of the things they talk about is introducing fraction concepts through contexts that give meaning to the fractional quantities. So I’m wondering, if kids are using an area model that is rooted in an accessible context (4 children are given 11 brownies to share, how much does each child get?), can our concerns about their formal understanding of “area” can be allayed somewhat? Thoughts?
It seems to me that it’s fine to have an intuitive notion of halves and quarters of circles without getting bogged down in considerations of area, so your cookie example would work that way. That’s what I had in mind with my original comment, and I read Peter Gould’s comment the same way when he says “I have no concerns about students using the terms halves and quarters (or fourths) in context”. Already with thirds, however, it can get tricky. There’s the standard error of diving the circle into three vertical stripes with equally spaced lines, for example. You can replace circular food with rectangular food, of course; but then it’s worth relating to area, it seems to me (e.g. a 9″ x 12″ cake shared out in various ways).
Basically I agree, and indeed this is one of the reasons CCSS introduces number lines and tape diagrams early.
Hi Bill,
On page 8, the second paragraph under decimals, it states “Grade 3 students learn to add decimal fractions by converting them to fractions with the same denominator…….” In third grade (3.NF.abc) equivalence of fractions is only for special cases. Where in the third grade standards do students add decimal fractions and convert fractions to the same denominator?
Shannon, that’s a typo, it should say “Grade 4 students …”. Thanks for pointing it out.
Hi Bill,
The standard in question is 5.NF.4b, in particular, the part “tiling it with unit squares of the appropriate unit fraction side lengths”. First, the term “unit square” has an important meaning “1 by 1 square”. For example, it is used in this sense in this document in the description of 4.NF.7 Was it the intention to use “unit square” also in the sense “uniform building blocks”. Additionally, here and other places (AZ and UT takes on the standards) “unit squares” are interpreted as rectangles with unit fraction side lengths, the denominators corresponding to the denominators of the side lengths of the original rectangle.
Personally, I feel that “unit square” should be reserved for “1 x 1” square, and the “unit square” in the standard should be understood as “rectangle with unit fraction sides lengths”. For example, 1/2 x 1/3 can be seen as one rectangle out of 6 and does not have to be seen as six 1/6 by 1/6 squares out of 36. I would appreciate the authors’ take here.
Thank you,
Alexei
Alexei, this is really a glitch in the standards. I agree that “rectangle with unit fraction side lengths” is what is meant. If you look on page 12 you’ll see that this is indicted by the diagram in the margin below where 5.NF.4b.
As a Math Coach who works primarily with middle school teachers, but occasionally with elementary school teachers, I thank you for these progressions documents! They are extemely helpful in guiding our thinking as we begin to plan our Common Core Math units. I do have a couple of questions.
– A question about the progressions in general:
I’m wondering if there is a timeframe for when the remainder of the progressons drafts and ultimately, the final version of the progressions documents, will be released? Do you anticipate that significant changes will be made to the draft documents?
– A question and a comment specific to the fractions document:
a) I recently had the opportunity to read through the fractions progressions with a group of 3rd – 5th grade teachers. We all were questioning the opening statement on p. 10 (grade 5): “In grade 4, students calculate sums of fractions with different denominators where one denominator …” I see that this was previously questioned back in Aug. 2011, however I am concerned with your response. As much as I appreciate the progressions, I believe the standards will be the primary resource used by educators; the grade 4 standard very clearly states that adding and subtracting of fractions will be done using like denominators. I am wondering if you might address this with a bit more detail? I have concerns that if the progressions documents do not clearly align with the standards, as they are written, the validity and value of the progressions will likely come into question. I am asking that you please take this into consideration as revisions are made.
b) I would like to share some of the responses from these teachers and also some of my MS colleagues who read the ratio/proportionality and the statistics progressions. Almost every teacher found value in these documents. They feel the progressions very clearly outline how to build understanding; the teachers stated that although some of the content may be similar to what they already teach, HOW they teach it will change. There was much concern voiced over how challenging it was to read through these documents. The MS teachers were able to work their way through and have rich converstations; they are content sprecialists. The elementary teachers, in some cases, needed some guidance working their way through the mathematics – which is truly written for someone who is comfortable with algebraic representation. I am a content specialist and I actually found the fractions document harder to read than the MS documents. Again, my concern is that if these are meant to be helpful to teachers as they plan their Common Core units, the elementary documents need to be written in a language that does not intimidate teachers who, themselves, do not have a comfort level with mathematics.
Thank you.
Patricia Posluszny
Patricia and Bill,
A follow-up to Patricia’s question about “In Grade 4, students calculate sums of fractions with different denominators where one denominator is a divisor of the other,…”
Adding fractions with different denominators does appear in CCSS-M Grade 4, but only as decimal fractions, with the example 3/10 + 4/100 = 34/100. My reading is the same as Patricia’s, that 1/3 + 1/6 is not there in the fourth grade.
North Carolina’s official commentary on the CCSS-M, the “Unpacked” series, uses the exact example here, 1/3 + 1/6, to interpret the fifth grade CCSS-M to instruct us to use 18 as the common denominator.
Please clarify.
To second Patricia Posluszny’s comment, the grade 4 standard does have addition of fractions with unlike denominators, but only decimal fractions, adding 3/10 + 4/100 = 34/100. (4.NF.5) The example in the Grade 5 section of the Progressions for 3-5 Number and Operations – Fractions of what students were supposed to have learned in fourth grade, 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2, is clearly not there in the CCSS-M.
In fact, North Carolina’s official commentary on the CCSS-M, the “Unpacked” series, uses this exact example, 1/3 + 1/6, to interpret the Grade 5 CCSS-M to say that the student should use 18 as the common denominator.
I hope you can clarify.
Note the footnote on 4.NF.5: “Students who can generate equivalent fractions can develop strategies for adding fractions with unlike denominators in general. But addition and subtraction with unlike denominators in general is not a requirement at this grade.” I agree the progression is a little misleading here.
Hi Bill,
I’m a math coach in Massachusetts and we use Everyday Math in our district. We’ve been having some good discussions around the fraction standards in K-3 and if or when fractions of collections should be introduced. I can’t find any direct mention of fractions of sets. As I read the standards and the progressions document I’m interpreting the emphasis to be on area and number line models – so where does that leave the set model? Could you clarify this? Thank you.
A natural place to consider set models would be Grade 5, where students start multiplying whole numbers by fractions, and so they could interpret
in terms of a set of 10 objects. As for introducing set models earlier, it was an intentional omission on the advice of reviewers, but I don’t think that should forbid curriculum developers from experimenting with various ways of introducing fractions. The argument against set models was that they didn’t fit well with the unit fraction approach. If children are used to counting objects, say 1, 2, 3, 4, 5 teddy bears, it’s confusing (so the argument goes) to turn around and declare 5 teddy bears to be a whole, so that one of them is 1/5 of the teddy bears, 2 of them are 2/5, and so on. There seems to be a shifting back and forth between 1 and 1/5/, 2 and 2/5, etc. On the other hand, it seems to me that this provides an opportunity to discuss the importance of specifying the whole when defining fractions, so I can see the value in set models earlier. As I said, I think this it is up to curriculum developers to work these things out; that which is not mentioned is not thereby forbidden.
Thank you for your response. I agree that the set model can lead students (and teachers) to misconceptions about fractions as two counting numbers. I find this especially true in grade 1. Later, perhaps by grade 2, the model makes more sense and can help develop some flexibility around the meaning of the whole. I think it’s interesting that the clarification was left to curriculum developers to experiment with –
I have taught or tutored mathematics at all levels, grade school through graduate school. I have a Ph.D. in mathematics. Most of my students need more knowledge of fractions. The Common Core standards omit the simplification of fractions. How do you measure 22/33 cup of milk? A standard measure is 2/3 cup. Suppose you want to convert 150 minutes to hours. The result is 150/60 hours, perhaps not a useful measure. Simplifying, you get 5/2 or, better, 2 ½ hours.
For adding and subtracting fractions, Common Core says
• 5.NF.1. Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (In general, a/b + c/d = (ad + bc)/bd.)
This algorithm is not efficient when adding three or more fractions. Here is a sample problem from a test given to people joining the military: “A baker made 20 pies. A Boy Scout troop buys one-fourth of this pies, a preschool teacher buys one-third of his pies, and a caterer buys one-sixth of his pies. How many pies does the baker have left? (reference below)”
With Common Core, you multiply all the denominators, getting 72, and add like this:
1/4 + 1/3 + 1/6 = (18 + 24 + 12)/72 = 54/72.
So 18/72 of the pies remain, and 20 * 18/72 = 360/72, not an acceptable answer on this test.
The Standards omit least common denominator, which is 12 in this example. Using it, the calculation becomes:
(3 + 4 + 2)/12 = 9/12 = ¾. So ¼ of the pies remain, and ¼ * 20 = 5, the correct answer.
Without the least common denominator, the calculation is slower and more likely to have mistakes; the result is unsimplified. The Standards include least common multiple, but why teach this idea and leave out its main use, least common denominator?
For mixed numbers, the standards say:
4.NF.3
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
I infer “and/or. . . .” means calculation without using improper fractions. Omit the word or. Both methods are important. The drafty-draft does not mention calculation of mixed numbers as such. Say you join 3 rods, of lengths
4 5/16, 2 1/16, and 3 7 /16 inches.
The efficient way to calculate the resulting length is to add the whole numbers, then the fractions, getting 9 13/16″. Common core method, with improper fractions:
69/16 + 33/16 + 55/16 = 157/16″.
Comparing the two methods, the calculation with improper fractions is slower and more likely to have mistakes; the sum is an improper fraction, which may not be as useful as a mixed number.
Skill with fractions is important in life. To enter the military, people take the Armed Forces Qualification Test, which includes fractions. Calculators are not allowed on the test. (See sample tests at http://www.military.com/join-armed-forces/asvab/). To become a contractor, people take a licensing examination, which includes fractions. Foreign countries, such as Singapore, teach simplification of fractions and least common denominator. See http://www.singaporemath.com/v/vspfiles/assets/images/sp_pmstdtg5a1.pdf.
Fractions are also basic to higher mathematics:
In trigonometry, the student may need to know that 5π/10 = π/2.
A formula for calculating exponential growth, with doubling time k, initial amount A, and time t, is A*2^(t/k). if an investment doubles every 8 years, how much does it grow in 24 years? The exponent here is 24/8. If the student simplifies this fraction as 3, they get 2^3 = 8; so if you start with $1000, you have $8000 in 24 years. If the student cannot simplify 24/8, the calculation requires a calculator.
Understanding numerical fractions, the student is ready for algebraic fractions
I admire the Common Core for promoting games and hands-on activities. It improves the standards of many states. Refine the standards. Students should learn to calculate fractions with speed and accuracy in grades through 5. Then they should also use fractions in middle and high school to maintain skill.
.
I admire Common Core for more emphasis on fractions than many schools now require. Also, I like the encouragement of activities and interesting applications. I hope you will include these three topics: least common denominators, calculation with mixed numbers as such, and simplification.
.
[Typo corrected 6/7/2012]
Elizabeth,
There’s a long discussion of this topic, with some responses already from Dr. McCallum, at the “General Questions about the Standards” site. Find “denominators” if you don’t want to scroll through the whole thing.
http://commoncoretools.me/2012/04/02/general-questions-about-the-standards/#comments
Thanks Brad for pointing out this link! I’ll answer a few of Elizabeth’s questions here that might not be addressed exactly in that link.
First, on simplification. The last sentence of the following standard is relevant here:
In both your examples it is reasonable to expect students to try to make sense of their answers by expressing them as 2/3 and 2 1/2, for the reasons you give. Thus, there is support in the standards for the answer you want.
On least common denominators, I think the other thread has most of what I want to say. I would just point out that the same principle as above applies to the answer 360/72; students are expected to make sense of their answers, in this case by finding an equivalent fraction that expresses better how many pies there are. Also, it’s not obvious to me that the extra efficiency of finding the least common denominator is worth the time taken in the curriculum by teaching it as a general method. And, as I said elsewhere, it is certainly not forbidden that students see and use that shortcut here.
On mixed numbers: the method you suggest for adding 4 5/16, 2 1/16, and 3 7 /16 is exactly what is intended by the phrase “using the properties of operations”. Namely, students should see 4 5/16 as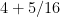
, etc., and then your method of adding the whole numbers first and then the fractions is just the principle that you can add numbers in any order and any grouping (commutative and associate laws of addition, although it is not necessary to use those terms). I completely agree that method is preferable.
For your last example, I agree that students should see that 24/8 = 3. Another relevant standard here, and also for the pie problem, is
Students should see that 24/8 is 24 divided by 8, and therefore 3 (from their knowledge of multiplication facts).
Thanks to Brad and Bill for thoughtful, prompt replies. I am glad that you agree, 2/3 of a cup is a more sensible measure than 22/33. Thank you for agreeing that it may be wise to add mixed numbers without conversion to improper fractions. The Standards seem to say this method is optional; rarely do I encounter a student who knows it. Both methods of addition/subtraction should be taught: with and without conversion. You also say ( http://commoncoretools.me/2012/04/02/general-questions-about-the-standards/#comments) “the Standards do not require simplifying fractions into lowest terms, since it is not a mathematically important topic. To quote the Fractions Progression, ‘It is possible to over-emphasise the importance of reducing fractions …. There is no mathematical reason why fractions must be written in reduced form, although it may be convenient to do so in simple cases.’” Please see my comments at the above link.
Page 8 of the NF Progressions document provides an example of multiplying a whole number by a mixed number in Grade 4. Is this an accurate example as the Standards only use the term “fractions” (4.NF.4c) not “fractions and mixed numbers” as is used elsewhere (5.NF.6).
Similarly, page 9 provides an example of converting a mixed number to a decimal fraction, and converting 2.70 to 2.7. Is this beyond what students should be doing? Should conversions be kept to amounts less than 1?
For the reply to this, please see the forum on the Fractions Progression.
This question was resubmitted by the poster to the fractions forum, and answered there.